
- Mathématiques
- Béton armé
- Résistance des Matériaux
- Mécanique
- Statique graphique
- Fatigue – Mécanique de la Rupture
- Chimie
- Bases scientifiques
- Thermodynamique
- Mécanique des fluides
- Science des Matériaux
Mathématiques
Formulaire du BAC S
Un formulaire très complet pour les mathématiques supérieures (post-bac)
Limites, continuité, dérivation, intégration, fonctions usuelles
Formule de Taylor, développements limités usuels, opérations sur les DL, calcul de limites et levée des formes indéterminées, position par-rapport à la tangente, étude des asymptotes
Intégrales doubles, théorème de Fubini, fonctions de la forme f(x,y)=g(x).h(y), intégrales triples, changement de variables, matrice jacobienne, changement de variable affine, cylindrique, sphérique, formule de Green Riemann, formule de Stokes, formule de Green-Ostrogradsky
Forme algébrique, forme trigonométrique, forme exponentielle, équations du second degré dans C
Equations à variables séparables, équations différentielles linéaires à coefficients constants du premier ordre et second ordre
Suites numériques, représentation graphique d’une suite, sens de variation, suite majorée/minorée/bornée, limite, suites adjacentes, suites arithmétiques, suites géométriques, suite arithmético-géométriques, relations de comparaison, séries de nombrées réels ou complexes, suites et séries de fonctions
Séries entières, convergence des séries entières, développement en série entière, résolution d’équations différentielles avec les séries entières, fonction périodique, série d’une fourier d’une fonction périodique
Rappels de dénombrement, binôme de Newton, calculs de probabilités, probabilités conditionnelles, évènements indépendants, théorème des probabilités totales, variables aléatoires, lois de probabilités, fonction de répartition, va discrète et continue
Notion de stratégie, équilibre de Nash, jeux à somme nulle, dilemme du prisonnier, jeux de coordination
Chaines de Markov, matrice de transition, graphe des transitions, comportement asymptotique, distributions stationnaires, chaines absorbantes
Statistiques descriptives, ajustements linéaires et non-linéaires, statistiques inférentielles
Test d’hypothèses, test bilatéral, test unilatéral, risques de première et deuxième espèce, test de comparaison d’une moyenne expérimentale à une moyenne théorique
Calcul propositionnel, raisonnements (direct, cas par cas, récurrence, par l’absurde, contre-exemple, contraposée)
Calcul booléen
PGCD, PPCM, décomposition d’un nombre entier en produit de facteurs premiers, équation de Bezout, congruence, codage RSA, jeux de type NIM
Espaces et sous-espaces vectoriels, combinaisons linéaires, famille libre, famille génératrice, base, application, rang, image, noyau, endomorphisme, espace euclidien, espace préhilbertien, Inégalité de Cauchy-Schwartz, Orthonormalisation de Gram-Schmidt, Projection orthogonale
Ensembles, applications, relations
Rappels sur les vecteurs, produit scalaire, produit vectoriel, produit mixte
Champ scalaire, champ vectoriel, gradient, divergence, rotationnel, laplacien
Matrices et calcul matriciel, systèmes linéaires
Matrices pour l’infographie, matrices de projection, matrices de transformation, compositions de transformations, changement de base, invariants, quaternions et rotations
Limites, continuité, dérivées partielles, différentielle, estimation au voisinage d’un point, développement limité, points critiques, recherche des extremums
Béton armé

Résistance des Matériaux
Hypothèses de la théorie des poutres, hyperstaticité interne/externe/globale, torseur de cohésion, caractéristiques géométriques des sections, contraintes, loi de comportement d’une poutre en flexion, systèmes hyperstatiques, poutres continues, méthodes énergétiques, flambement, rappels sur les propriétés mécaniques des matériaux
4 exercices :
- Moment d’une force
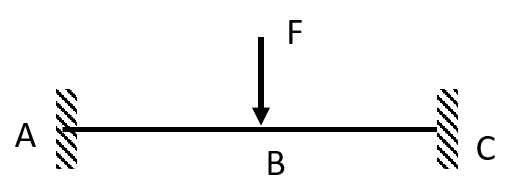
- Poutre en flexion avec appui mobile
- Déformation d’un pilier sous son poids propre
- Solide d’égale résistance
Mécanique
Outils mathématiques pour la MMC, cinématique, déformations d’un milieu continu, contraintes, dynamique des milieux continus, lois et équations de bilan de la MMC, loi de comportement fluide / solide
Mécanique du point : cinématique, dynamique, énergétique, changement de référentiel, quantité de mouvement
Etude des mécanismes, statique, cinématique, cinétique, dynamique, énergétique, équilibrage, stabilité
Mécanique analytique, équations de Lagrange
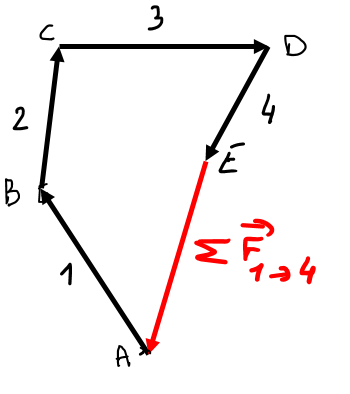
Statique graphique
Polygone des forces, polygone funiculaire, étude des poutres, treillis, épure de Cremona, cinématique graphique

Fatigue – Mécanique de la Rupture

Chimie
Acides bases, oxydoréduction, cinétique chimique
Bases scientifiques
Thermodynamique
Mécanique des fluides
Rappels de mécanique des fluides, exercices de statique et dynamique des fluides
Science des Matériaux
Structure de la matière, cristallographie, défauts dans les cristaux, diagrammes de phases
Propriétés mécaniques, thermiques, électriques, choix des matériaux
Microscopie optique et électronique, analyses (calorimétrie, granulométrie, dilatométrie……)
Familles de matériaux métalliques, système Fe-C, traitements thermiques, relations microstructure/propriétés mécaniques, alliages d’alu, métaux pour l’emballage
Matériaux métalliques : exercices
Polymères et composites
Céramiques, matériaux divers

Frédéric Menan – Enseignant responsable pédagogique CESI Brest
2025