Retrouvez maintenant les vidéos du site sur la chaine Youtube @lesdocsduprof !
Blog
-
Dimensionnement des poutres
Ne pas rompre sous les efforts à supporter, c’est essentiel….. Mais ne pas trop se déformer, c’est important aussi.
Un exemple récent :
Millenium Bridge de Londres
-
6 méthodes pour apprendre et mémoriser plus efficacement !
Une infographie learningscientists.org qui décrit 6 méthodes pour apprendre et retenir vos apprentissages plus efficacement. Je vous les conseille !
Ces méthodes sont basées sur des principes éprouvés, par exemple :
- Pour qu’une info reste aussi longtemps que possible en mémoire, il faut la revoir plusieurs fois, à des périodes espacées dans le temps.
- Pour graver à long terme une information dans votre mémoire, la meilleure méthode est la récupération. Plutôt que de lire l’information, il vaut mieux forcer votre mémoire à aller chercher cette information avec un quiz, une explication à un camarade, en dessinant cette info ou en essayant de réciter votre cours à voix haute.
- Discuter avec une autre personne permet d’aborder des notions à la fois à l’écrit et à l’oral, ce qui aide à mémoriser. Idem quand on dessine, schématise, une une notion théorique. Une info codée de plusieurs manières différentes sera mieux mémorisée.
Référence : https://www.learningscientists.org/poster-translations
-
« TAF : Tableau des Actions à Faire » : un livre que je recommande !
Dans son ouvrage « TAF : tableau des actions à faire », Hughes GISSLER propose une méthode de gestion du temps et d’organisation personnelle novatrice et pertinente.
Après quelques tests pour s’évaluer sur sa charge de travail et son organisation, les 9 principes de la méthode TAF sont énoncés et la mise en pratique est expliquée. L’auteur propose aussi quelques outils d’organisation, de développement personnel, de communication et de gestion du stress qui viennent compléter la méthode TAF.
Mais c’est quoi TAF ?
Pour le découvrir il faudra vous procurer le livre mais je peux essayer de vous donner un avant-gout.
Disons que vous avez une montagne à gravir (1 mois), un rapport à écrire (2 jours) et un projet à redéfinir avec des collègues. Noter « gravir la montagne », « écrire rapport » et « redéfinir projet » sur une liste, c’est facile mais pas très motivant. Ça ne dit pas par quoi, comment, et pour quand et on se retrouver avec une longue liste de tâches assez effrayante. Alors qu’écrire « acheter chaussures de randonnée avant l’ascension de printemps », « lister éléments à résumer dans le rapport » et « trouver une date pour prochaine réunion projet », c’est déjà plus facile, non ?
La méthode TAF et mon expérience personnelle
Fainéant par nature, devenu partisan du moindre effort parce qu’il faut bien bosser un peu, je pense faire naturellement un peu de méthode TAF. J’ai toujours plus réfléchi à « quelle action me permettrait de me débarrasser le plus rapidement de ce truc ? », plutôt que « je dois prévoir 3h pour ça ». TAF améliore votre organisation en étant résolument orientée vers l’action.
Je me démoralise facilement quand je dois réaliser une tâche conséquente et peu intéressante ou qui n’a pas vraiment de sens pour moi. Alors je me répète « Rome ne s’est pas faite en un jour », « agir rend heureux », et je me lance dans cette tâche par une petite action, même minime. Je dois réparer cette micro-fuite dans ma toiture ? Plutôt que de ruminer pendant des semaines, je retrouve le numéro du couvreur près de chez moi puis je passe à autre chose. J’appellerai lors de ma prochaine fenêtre de surmotivation, qui n’arrive qu’une fois par semaine…. Mais les choses avancent ! J’ai l’impression que c’est un peu ça, TAF.
Alors jetez-vous sur ce livre ! Ou plutôt non, commencez par noter sur votre liste « acheter TAF » 😉
Frédéric Menan
H. Gissler, TAF, tableau des actions à faire: la méthode de gestion du temps qui transforme le stress en énergie. Malakoff: Dunod, 2024
-
Chiffres significatifs
Comment présenter correctement un résultat ?
Comment manipuler correctement des résultats numériques pour ne faire trop d’approximation dans les calculs ?
Dans l’exemple ci-dessous, on calcule la masse d’un cylindre en faisant des arrondis et en injectant la valeur arrondie dans un nouveau calcul. Les arrondis s’accumulent et on obtient une erreur de 6% sur la masse réelle du cylindre.
Le calcul formel présenté permet de n’effectuer qu’une seule application numérique donc sans arrondis.
Pourquoi raisonner en littéral (avec les symboles et pas les valeurs) ?
Conclusion
Il ne faut surtout pas
Faire les applications numériques intermédiaires et injecter le résultat arrondi dans la formule suivante car les arrondis s’accumulent et la valeur finale s’éloigne de la valeur réelle.
Mêler de l’application numérique et du littéral car les calculs deviennent illisibles.
Les bonnes habitudes
Définir toutes les variables si elles ne sont pas déjà définies.
Réaliser tout le calcul en “littéral” puis réaliser l’application numérique et presenter le résultat final avec un nombre de chiffres significatif cohérent.
Présentation d’un résultat : choix du nombre de chiffres significatifs
•Le résultat d’un calcul ne peut être exprimé avec une précision supérieure à celle de la donnée utilisée connue ayant la plus faible précision
•Addition / soustraction : le résultat ne peut pas avoir plus de décimales que le terme qui en comporte le moins
•Multiplication / division : le résultat ne peut pas avoir plus de chiffres significatifs que le terme qui en comporte le moins
Les chiffres autres que zéro sont toujours significatifs.
Le zéro n’est pas significatif quand il est à gauche des autres chiffres. Il est significatif si placé à droite.
Un entier a un nombre infini de chiffres significatifs
Choix de la valeur arrondie
•Si le premier chiffre enlevé <5, dernier chiffre inchangé
•Si le premier chiffre enlevé >5 ou=5 suivi de chiffres ≠ 0, dernier chiffre restant augmenté de 1
•Si le premier chiffre enlevé =5 suivi de zéros, dernier chiffre inchangé s’il est pair, augmenté de 1 si impair
-
Dimensionnement du viaduc de Garabit par Gustave Eiffel à l’aide du théorème des trois moments (ou théorème de Clapeyron)
Un bel exemple de calcul d’une poutre continue par le théorème des trois moments, calcul signé Gustave Eiffel.
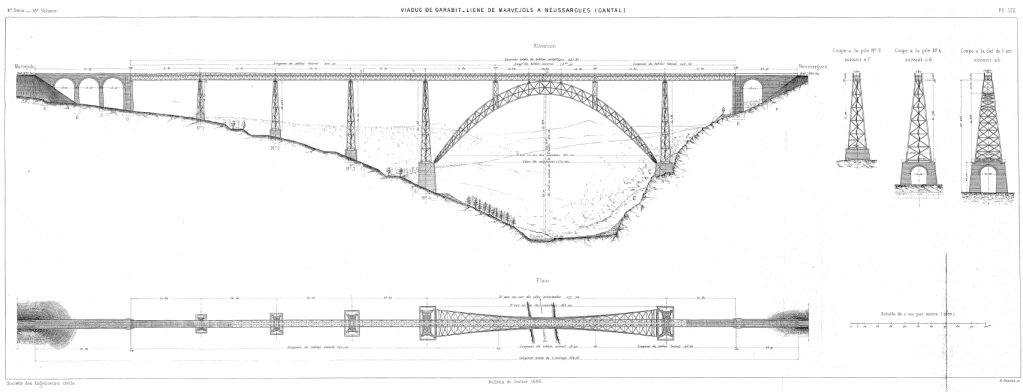
La poutre continue dispose de 5 travées ce qui rend les calculs des moments sur appuis assez fastidieux mais des tables numériques étaient données à l’époque (j’y reviendrai dans un prochain article).
Références
http://cnum.cnam.fr/redir?ECCMC6.49
Images anciennes : source Conservatoire National des Arts et Métiers, Conservatoire numérique https://cnum.cnam.fr
Photo B Godart, mai 2023 2023 – Frédéric Menan
-
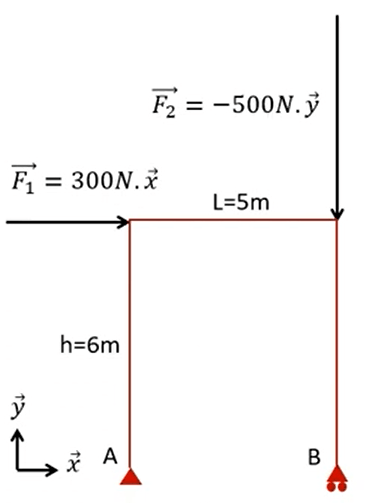
Une nouvelle vidéo de statique graphique : cas d’un portique
Dans cette nouvelle vidéo je vous propose le calcul des réactions d’appui dans un portique isostatique, par statique graphique.
L’avantage de la statique graphique est que l’on peut « voir » l’intensité et la direction des réactions d’appui.
Deux cas sont proposés avec les mêmes forces appliquées mais en des points différents. La statique graphique aide à visualiser l’évolution des réactions d’appui entre chaque cas.
2023 – Frédéric Menan
-
Exemples de fiches de révision
Quelques exemples de fiches de révision pour montrer aux étudiants ce qu’ils peuvent mettre en place pour synthétiser leurs cours.
2023 – Frédéric Menan
-
« Dit comme ça » épisode 1 : le logarithme
Le logarithme décimal est défini dans certains ouvrages par loga(x) = ln(x) / ln(a). Dit comme ça, ce n’est pas forcément très parlant !
Dans un ouvrage de 1967 j’ai trouvé une façon intéressante d’aborder le logarithme décimal :
Dit comme ça, on comprend la « construction » du logarithme : la fonction telle que log(10x)=x.
Mais on comprend aussi mieux une des utilisations de cette fonction : ramener sur un même graphe des valeurs se promenant sur plusieurs ordres de grandeurs.
Exemple. Si on trace le jeu de données ci-dessous les premiers point sont « écrasés » sur l’axe des ordonnées.
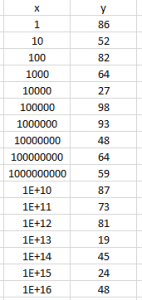
En traçant en abscisse log(x) et non x, les données deviennent bien plus lisibles.
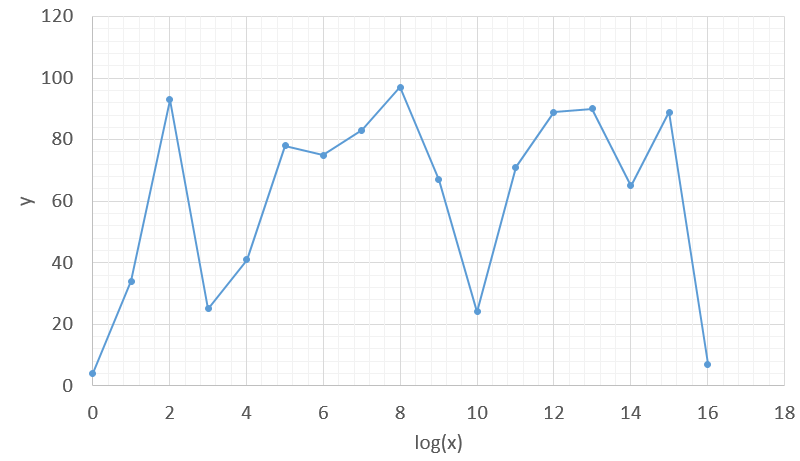
En général on placera une échelle logarithmique comme ci-dessous.
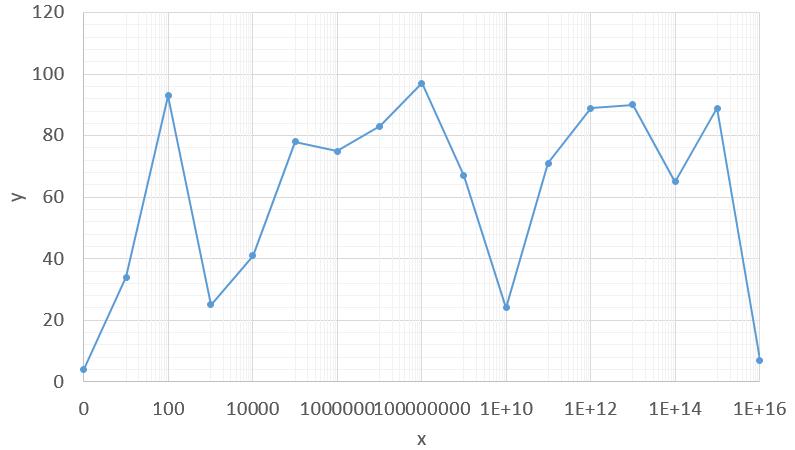
On comprend aussi aisément les propriétés usuelles du logarithme :
Références
« Algèbre ». R. Cluzel H. Court. Librairie Delagrave. 1967
2023 – Frédéric Menan
-
Statue de la Liberté : protection à la corrosion
Bibliothèque nationale de France Références
« La statue de la liberté éclairant le monde ». Talansier, Charles « Le Génie civil » (Paris). 1883. Doc Bibliothèque nationale de France
2023 – Frédéric Menan
Les Docs du Prof 