Blog
-
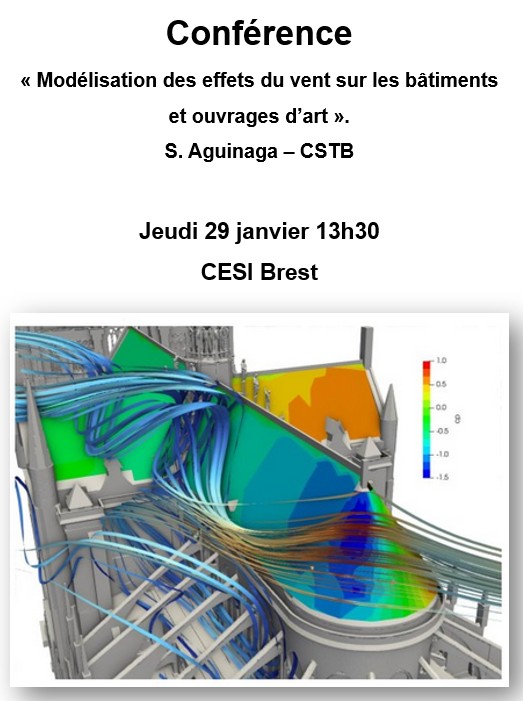
Conférence club Génie Civil Jeudi 8 janvier 2026
« La statique graphique : résoudre un problème de statique par le dessin »
Jeudi 8 janvier 2026 – 13h30
CESI Brest – salle 104
Chers étudiants du CESI Brest, dans le cadre du club Génie Civil j’animerai une conférence ce jeudi 8 janvier 2026 sur le campus, sur la statique graphique. Venez nombreux !!!

Résumé de la conférence
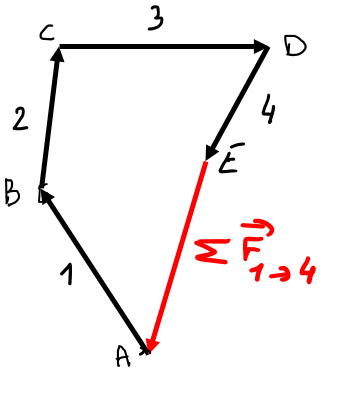
La statique graphique est une méthode de résolution par le dessin des problèmes de statique d’un système matériel.
Après une présentation du principe de la statique graphique, un historique de la statique graphique sera proposé. Les fondations de cette discipline sont érigées à partir du XVIe siècle et ses développements atteignent leur apogée à la fin du XIXe.
Dans un second temps, on verra que la statique graphique s’estompe tout le long du XXe siècle, au profit des méthodes analytiques et numériques, avant de redevenir un axe de recherche innovant pour le calcul des structures, en génie civil et architecture.
-
Influence d’un contreventement
Petite image sympa avant de partir en congés : l’influence d’une barre diagonale sur un cadre en spaghetti !

Sur la photo de gauche, on voit que les points de colle aux appuis laissent le spaghetti avoir un peu de rotation (si aux appuis la colle ne bloquait pas du tout la rotation, le système aurait un mouvement de solide rigide….). Ci-dessous on a renforcé la liaison aux appuis, on voit aussi l’importance sur la déformée.

Bonnes fêtes à tous !
-

1 kg avec 6 spaghettis ! (et un peu de colle)
Après le pont à haubans de cet été avec du fil et du carton, j’expérimente les treillis en spaghetti !
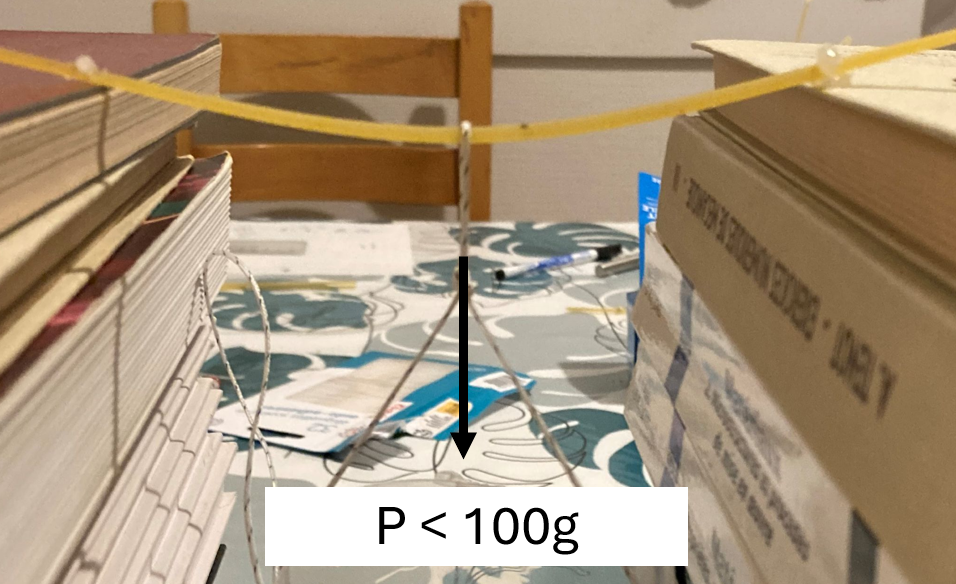
Si l’on prend deux spaghettis, qu’on en fait un petit pont de longueur 19,2 cm, et qu’on applique un poids au milieu, le poids maximal n’est pas fameux : 100g…..

De plus la raideur en flexion est très faible.

Alors comment renforcer cette poutre ?
Avec un treillis de spaghettis ! Dans certains cas on parle aussi de ferme.
Essai 1



Côté raideur, le treillis renforce les deux spaghettis de façon spectaculaire.

Côté résistance, on a multiplié la masse par 4, mais on a multiplié la résistance par 10.
Poutre 2 spaghettis Ferme Masse structure (g) 2 8 Charge maximale (kg) 0,100 1,002 Essai 2
Une structure moins résistante mais deux fois moins lourde, avec les deux barres diagonales fonctionnant en compression et la barre verticale en traction.
La résistance ramenée à 1g de spaghetti est globalement la même que pour l’essai 1.
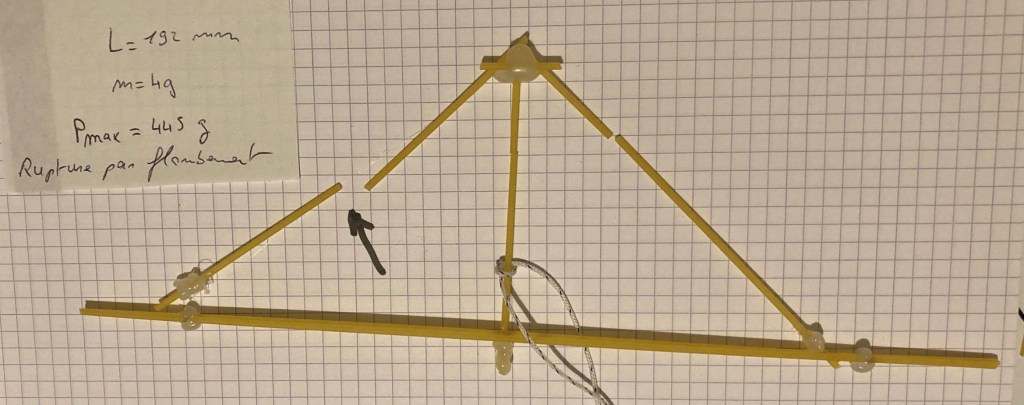
Autres essais
Ci-dessous des photos d’autres structures.



-
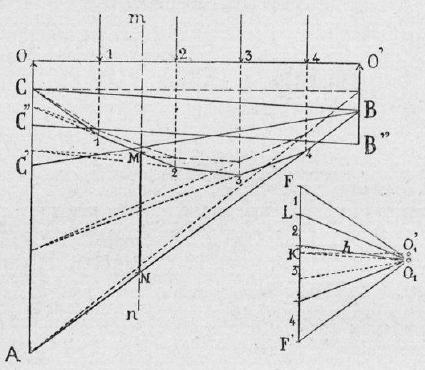
Publication sur la statique graphique dans la revue e-Phaïstos
Mon article sur l’histoire et l’actualité de la statique graphique est paru dans la revue d’histoire des techniques e-Phaïstos !
Ci-dessous le lien :
https://journals.openedition.org/ephaistos/14628


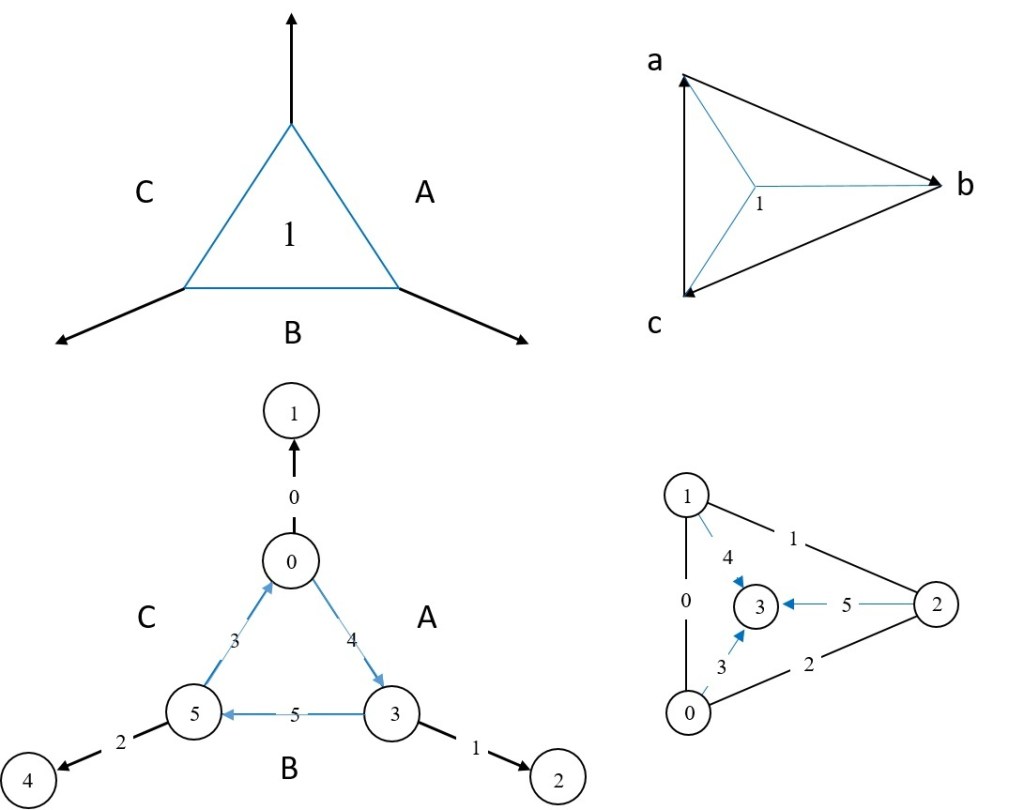
Résumé
La statique graphique est une méthode de résolution par le dessin des problèmes de statique d’un système matériel. Dans cet article, on propose d’illustrer l’oubli progressif de cette méthode lors du XXe siècle et le regain d’intérêt qu’elle connait aujourd’hui grâce à son intégration dans les outils numériques. Dans un premier temps, un historique de la statique graphique est proposé. Les fondations de cette discipline sont érigées à partir du XVIe siècle et ses développements atteignent leur apogée à la fin du XIXe. Dans un second temps, on verra que la statique graphique s’estompe tout le long du XXe siècle, au profit des méthodes analytiques et numériques, avant de redevenir un axe de recherche innovant pour le calcul des structures 3D, les matériaux cellulaires, les pièces imprimées et même le béton armé, grâce la représentation mathématique et numérique de ses fondements théoriques.
-

Projet Garabit : publication des résultats
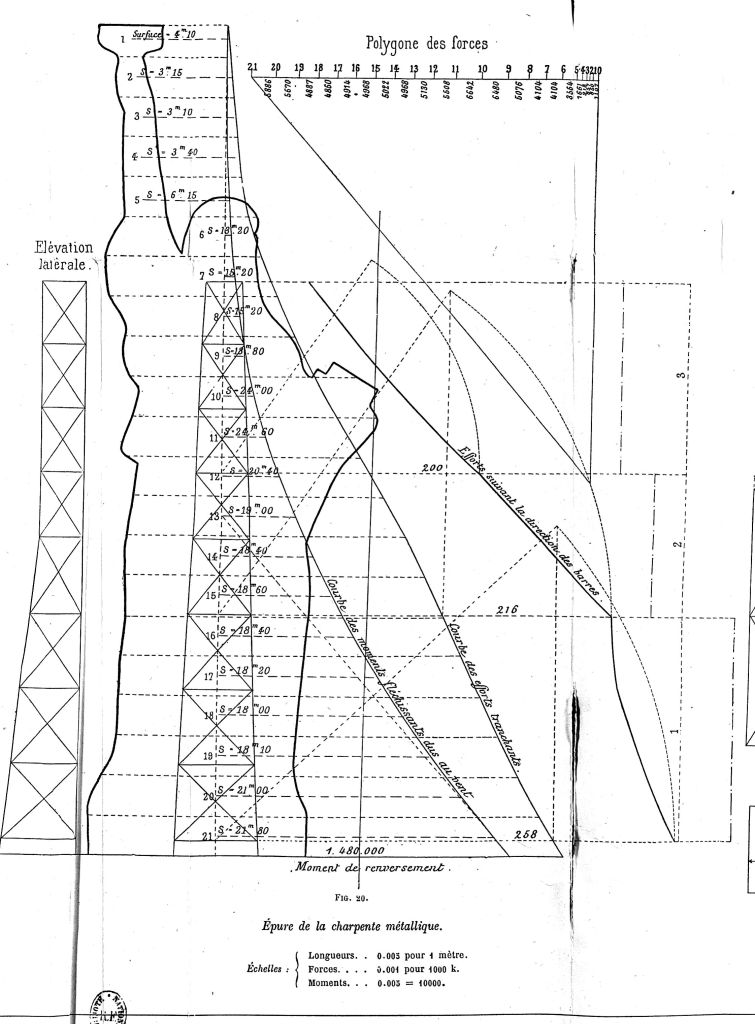
J’ai le plaisir de vous présenter une partie de mes travaux sur le dimensionnement du calcul de Garabit par Gustave Eiffel !

Ce projet est né d’une idée un peu folle : refaire et décrire tous les calculs réalisés par Eiffel sur le viaduc de Garabit, analyser les hypothèses réalisées par Eiffel, et proposer une perspective historique sur la construction de ce viaduc.
J’étudie les point suivants, conformément au mémoire original d’Eiffel :
Calcul des tabliers
- Tables horizontales des poutres principales : calculées comme des poutres continues
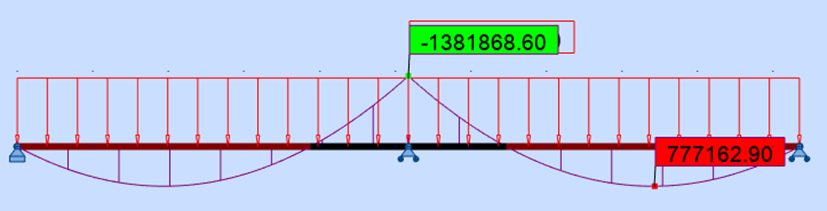
- Treillis des poutres principales
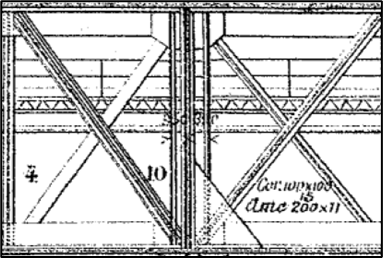
- Pièces de pont et longerons
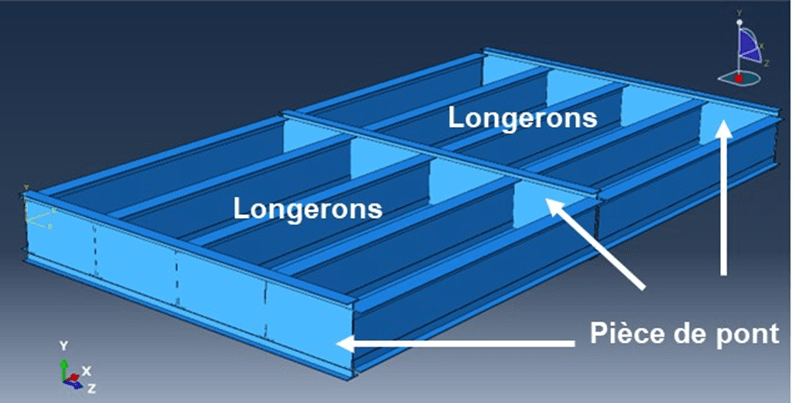
- Panneaux sur les appuis
Calcul des piles métalliques
- Section des arbalétriers
- Sections des croisillons

- Tirants d’amarrages
- Maçonneries
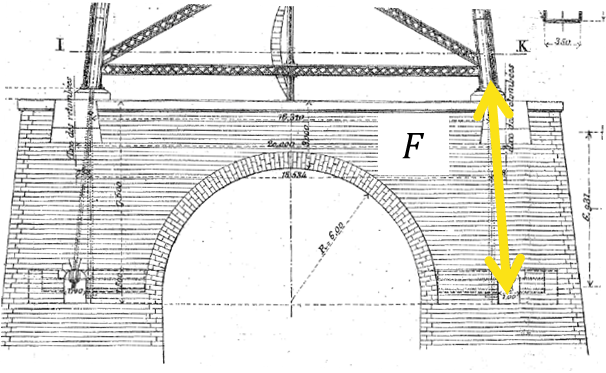
Calcul de l’arc
- Sections des membrures
- Sections des barres de treillis et des barres de contreventement
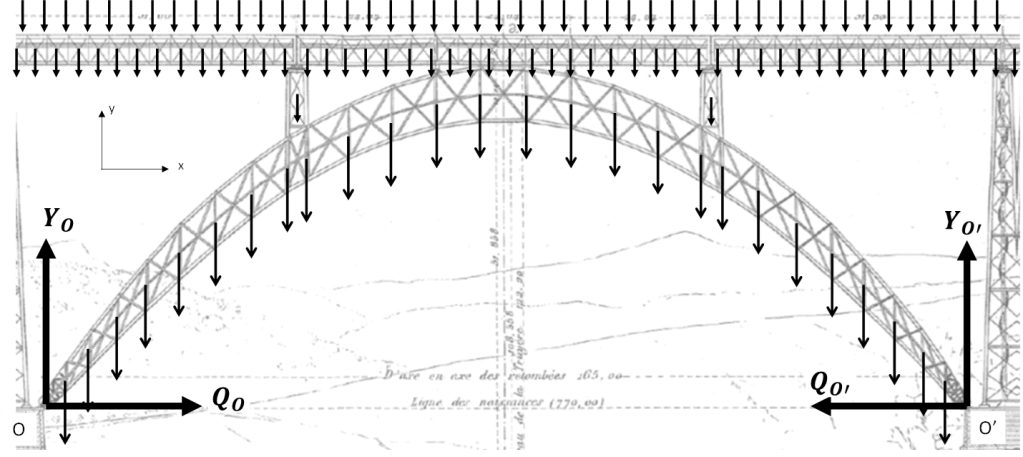
- Stabilité au vent
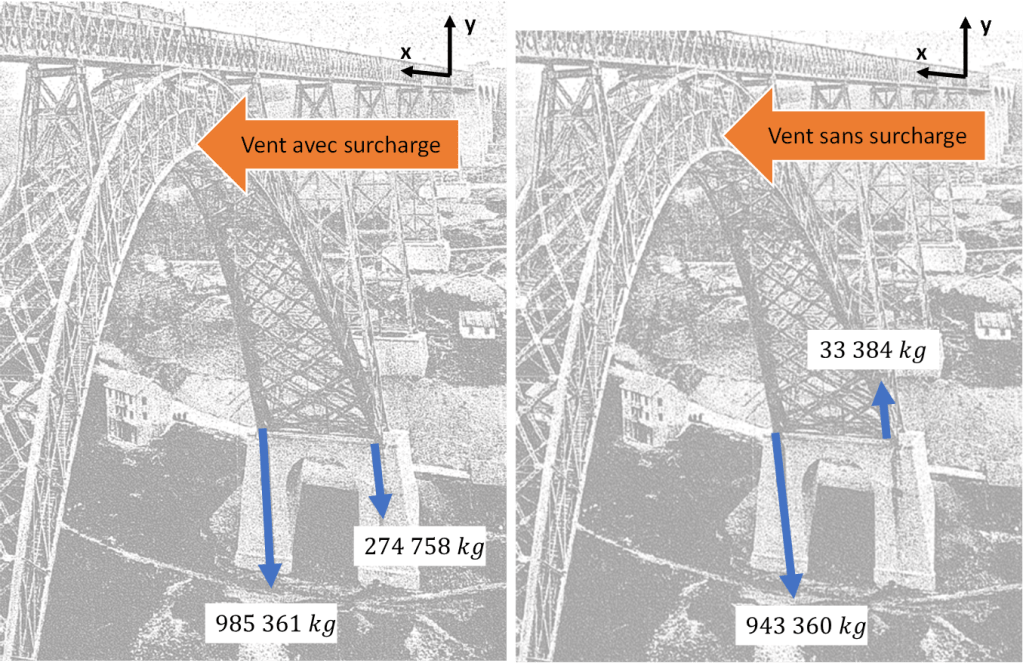
Les étudiants pourront découvrir une application concrète des notions de structures et matériaux qui leur sont enseignées. Les enseignants glaneront des exemples et exercices à présenter à leurs élèves. Les professionnels du génie civil affuteront leur culture générale sur ce passionnant domaine. Les néophytes pourront découvrir les méthodes de conception de ce type ouvrages d’art du génie civil.
Retrouvez les résultats dans le lien ci-dessous :
https://lesdocsduprof.com/projet-garabit/
2025 – Frédéric Menan
-

Club Génie Civil du CESI Brest : lancement de la saison 2025-2026 le 2 octobre 2025 !
Chers étudiants du CESI Brest, le club Génie Civil du campus lance sa saison 2025-2026 ce jeudi 2 octobre à 13h30.
Nous discuterons des activités possibles, du cycle de conférences de l’année, des visites prévues et de l’emploi du temps des séances.
Venez nombreux !

-

Bref, on s’est construit un pont à haubans !
Entre deux baignades, il faut bien s’occuper les idées, alors on s’est construit un pont à haubans avec un vieux carton et des morceaux de table qui trainaient !



Il a un petit côté pont de l’Iroise à Plougastel.

https://commons.wikimedia.org/wiki/File:Pont_de_l%27Iroise_-_2024.jpg#filelinks Dans un pont à haubans, ou pont haubané, le tablier (dans notre cas, un carton d’emballage) est suspendu à des haubans (les fils blancs), fils soutenus par des pylônes (dans notre cas, les morceaux de bois).
On a choisi un haubanage en semi-éventail, on voulait juste faire passer les fils entre les deux fixations des pylônes (ils sont constitués de deux morceaux de bois vissés). Les fils sont continus d’un point du tablier au point opposé, c’était nettement plus rapide à construire…

Les câbles sont placés dans le plan médian du pont, « en nappe centrale unique ».


Les haubans sont accrochés au tablier par des cales en plastique de meubles (qui trainaient dans une boite, vous l’aurez compris 🙂 ). De l’autre côté, des trombones permettent de faire coulisser le point d’attache et donc de régler la tension du câble.


Des premières épreuves de mise en charge ont été menées avec des gros camions, comme pour les vrais ponts sur les épreuves définitives. Admirez les gros camions ci-dessous !


Les épreuves finales ne sont pas très honnêtes car on n’a pas de rigidité en torsion donc on a du équilibrer les charges et on a un peu encastré aux culées avec un livre, mais enfin il faut se dire que le poids total soutenu (tasses, verres et boites de conserves) est déjà certainement supérieur au poids du pont.

Ce qui est intéressant c’est de se rendre compte de la problématique de la torsion du tablier, de la tension de chaque câble, des vibrations qui peuvent apparaitre sous l’effet du vent…..
Bon allez, à la baignade !
Quelques références
C2675 Ponts métalliques – Conception générale. Jean-Pierre DUCOUT. Collection Techniques de l’Ingénieur
C2676 Ponts métalliques – Applications spécifiques. Jean-Pierre DUCOUT. Collection Techniques de l’Ingénieur
https://fr.wikipedia.org/wiki/Pont_%C3%A0_haubans
-
Nouveau document : cahier d’exercices de RDM
Un nouveau document dans la page « Cours et exercices corrigés » : un cahier d’exercices corrigés de Résistance des Matériaux !
-

Limites et dangers de l’IA à travers des exemples concrets
Suite à un post Linkedin où je parlais de l’utilisation de l’IA, plusieurs étudiants m’ont répondu que nous devrions sensibiliser et former plutôt que de seulement dire « attention à l’IA ».
C’est vrai ! Alors je me suis lancé.
Je ne suis pas un expert de l’IA donc je suis parti d’exemples concrets et j’ai apporté mes remarques. Elles n’engagent que moi, c’est mon avis, à chacun de se faire le sien. 🙂
Ce travail est en cours de réalisation et le guide va évoluer, ce n’est qu’une version « à l’instant t. »
Si vous avez des suggestions ou des exemples, n’hésitez-pas à me contacter !