A retrouver sur la page de ressources 🙂
Étiquette : Mathématiques
-

Maths et IA générative : comment vous dire…. ?
Les applications possibles de l’IA ne sont plus à démontrer : recherche, médecine, aide à la conduite, génération de texte brut….. Avec des résultats pas toujours au rendez-vous. Et en maths ? Eh bien……
Sur le site lesdocsduprof, je peux demander à une IA de me générer des images.
Alors je ne sais pas si ça utilise chattruc4.7, Irobv12-3 ou GoogeulKL-42 et je m’en fous un peu.
Je vous laisse apprécier le résultat ! (je vais quand même essayer de rebondir un peu sur l’image générée)
Oui oui j’entends déjà les commentaires, j’ai pas fait les bons prompts, vous proposez de me former, tout ça tout ça……… 🙂
Prompt : théorie des ensembles

Soit E un ensemble d’amis autour d’une table……..
Prompt : processus stochastiques

Une vision idyllique de la théorie des files d’attentes ?
Prompt : calcul matriciel et quaternions

Ce quaternion a remporté le dernier prix à Longchamp je crois.
Prompt : séries de Fourier
Là j’avoue c’est top ! Impeccable !
Prompt : statistiques descriptives
Là aussi, c’est bien !
Prompt : équation différentielle
J’ai vu pas mal d’élèves taper des choses incompréhensibles au tableau à la simple vue du terme « équation différentielle » mais là, c’est du lourd !
Prompt : système linéaire

Ah oui c’est très très linéaire……
Prompt : soit x tel que 2x+3=0, calculer x

Avec une telle équation on a tous une bonne migraine alors une aspirine svp !
Prompt : cosinus

Il est où le côté opposé ???
Et un dernier pour la route : théorème de pythagore

Hypoténuse fut sa muse ?
Garanties sans trucage (première image obtenue dans tous les cas)
-
Chiffres significatifs
Comment présenter correctement un résultat ?
Comment manipuler correctement des résultats numériques pour ne faire trop d’approximation dans les calculs ?
Dans l’exemple ci-dessous, on calcule la masse d’un cylindre en faisant des arrondis et en injectant la valeur arrondie dans un nouveau calcul. Les arrondis s’accumulent et on obtient une erreur de 6% sur la masse réelle du cylindre.
Le calcul formel présenté permet de n’effectuer qu’une seule application numérique donc sans arrondis.

Pourquoi raisonner en littéral (avec les symboles et pas les valeurs) ?


Conclusion
Il ne faut surtout pas
Faire les applications numériques intermédiaires et injecter le résultat arrondi dans la formule suivante car les arrondis s’accumulent et la valeur finale s’éloigne de la valeur réelle.
Mêler de l’application numérique et du littéral car les calculs deviennent illisibles.
Les bonnes habitudes
Définir toutes les variables si elles ne sont pas déjà définies.
Réaliser tout le calcul en “littéral” puis réaliser l’application numérique et presenter le résultat final avec un nombre de chiffres significatif cohérent.
Présentation d’un résultat : choix du nombre de chiffres significatifs
•Le résultat d’un calcul ne peut être exprimé avec une précision supérieure à celle de la donnée utilisée connue ayant la plus faible précision
•Addition / soustraction : le résultat ne peut pas avoir plus de décimales que le terme qui en comporte le moins
•Multiplication / division : le résultat ne peut pas avoir plus de chiffres significatifs que le terme qui en comporte le moins
Les chiffres autres que zéro sont toujours significatifs.
Le zéro n’est pas significatif quand il est à gauche des autres chiffres. Il est significatif si placé à droite.
Un entier a un nombre infini de chiffres significatifs
Choix de la valeur arrondie
•Si le premier chiffre enlevé <5, dernier chiffre inchangé
•Si le premier chiffre enlevé >5 ou=5 suivi de chiffres ≠ 0, dernier chiffre restant augmenté de 1
•Si le premier chiffre enlevé =5 suivi de zéros, dernier chiffre inchangé s’il est pair, augmenté de 1 si impair
-
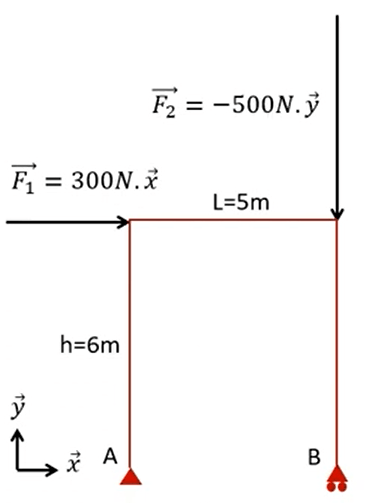
Une nouvelle vidéo de statique graphique : cas d’un portique
Dans cette nouvelle vidéo je vous propose le calcul des réactions d’appui dans un portique isostatique, par statique graphique.
L’avantage de la statique graphique est que l’on peut « voir » l’intensité et la direction des réactions d’appui.
Deux cas sont proposés avec les mêmes forces appliquées mais en des points différents. La statique graphique aide à visualiser l’évolution des réactions d’appui entre chaque cas.
2023 – Frédéric Menan
-
Exemples de fiches de révision
Quelques exemples de fiches de révision pour montrer aux étudiants ce qu’ils peuvent mettre en place pour synthétiser leurs cours.
2023 – Frédéric Menan
-

« Dit comme ça » épisode 1 : le logarithme
Le logarithme décimal est défini dans certains ouvrages par loga(x) = ln(x) / ln(a). Dit comme ça, ce n’est pas forcément très parlant !
Dans un ouvrage de 1967 j’ai trouvé une façon intéressante d’aborder le logarithme décimal :


Dit comme ça, on comprend la « construction » du logarithme : la fonction telle que log(10x)=x.
Mais on comprend aussi mieux une des utilisations de cette fonction : ramener sur un même graphe des valeurs se promenant sur plusieurs ordres de grandeurs.
Exemple. Si on trace le jeu de données ci-dessous les premiers point sont « écrasés » sur l’axe des ordonnées.
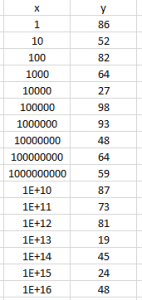

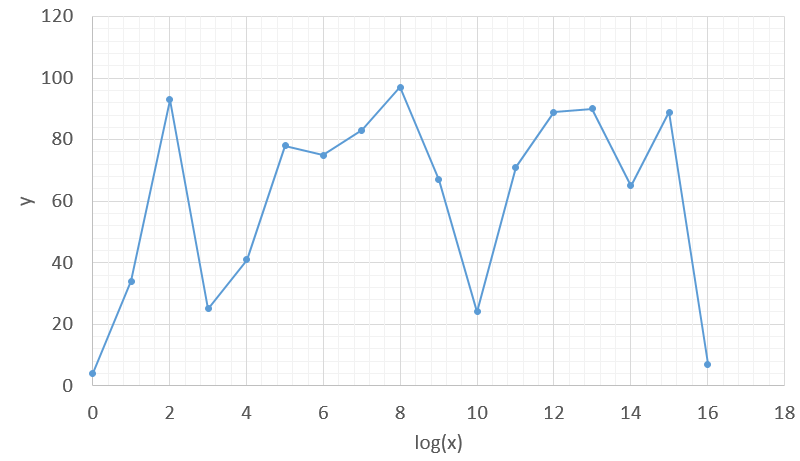
En traçant en abscisse log(x) et non x, les données deviennent bien plus lisibles.
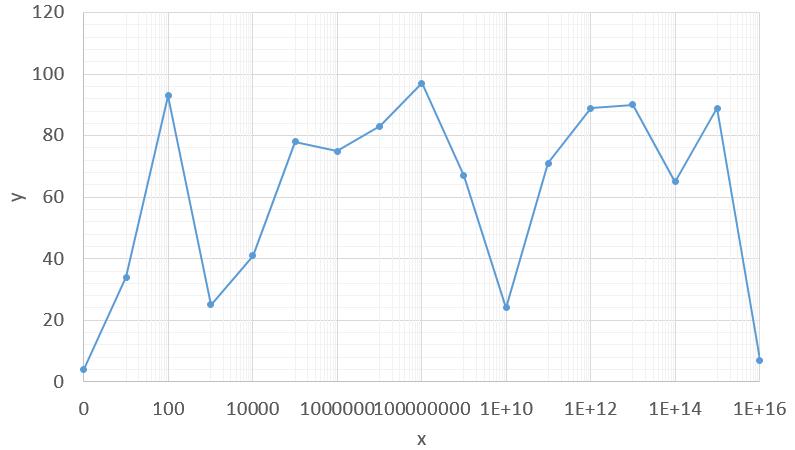
En général on placera une échelle logarithmique comme ci-dessous.
On comprend aussi aisément les propriétés usuelles du logarithme :


Références
« Algèbre ». R. Cluzel H. Court. Librairie Delagrave. 1967

2023 – Frédéric Menan