Le logarithme décimal est défini dans certains ouvrages par loga(x) = ln(x) / ln(a). Dit comme ça, ce n’est pas forcément très parlant !
Dans un ouvrage de 1967 j’ai trouvé une façon intéressante d’aborder le logarithme décimal :


Dit comme ça, on comprend la « construction » du logarithme : la fonction telle que log(10x)=x.
Mais on comprend aussi mieux une des utilisations de cette fonction : ramener sur un même graphe des valeurs se promenant sur plusieurs ordres de grandeurs.
Exemple. Si on trace le jeu de données ci-dessous les premiers point sont « écrasés » sur l’axe des ordonnées.

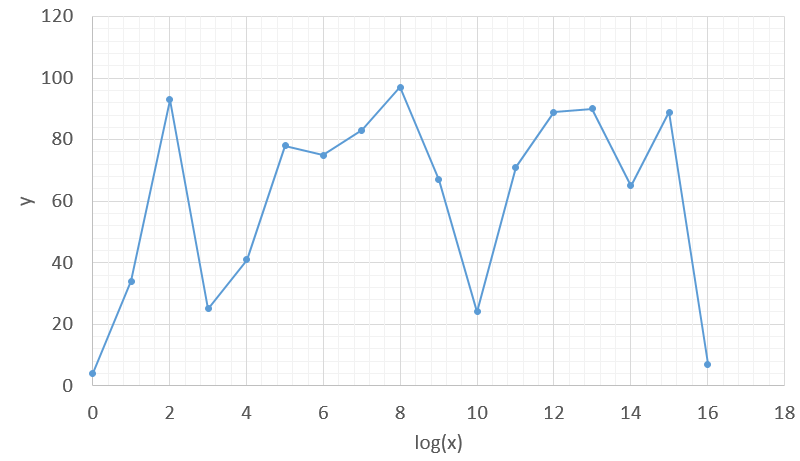
En traçant en abscisse log(x) et non x, les données deviennent bien plus lisibles.
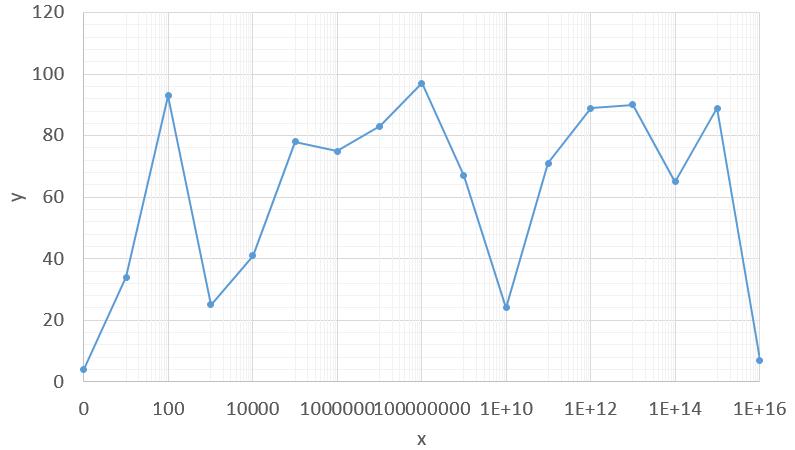
En général on placera une échelle logarithmique comme ci-dessous.
On comprend aussi aisément les propriétés usuelles du logarithme :


Références
« Algèbre ». R. Cluzel H. Court. Librairie Delagrave. 1967

2023 – Frédéric Menan